
Golden Ratio and Fibonacci Numbers in Mathematics
Golden Ratio (phi – φ) in mathematics is an amazing magical number. It is hidden in almost everything that we see around us! Let us see, what is so special about the golden ratio and its relationship with Fibonacci Numbers, in this section.
The value of golden ratio (phi – φ) is approximately equal to 1.618.
Golden Ratio in world’s most popular creations
If the ratio between different regions of someone’s face is 1.618, as shown in the figure-1 above (i.e., a/b = 1.618; “a” and “b” are shown in figure-1), it means he / she has a perfect good-looking face.
The structures / architectures / paintings that are created in golden ratio are said to have the most beautiful form.
The golden ratio was used in the ancient Greek architecture. The ratio between the width of base (756 ft) and height (481 ft) of pyramids of Giza, is said to be 1.6 approximately. Also, the Italian polymath Leonardo Da Vinci is said to have used the golden ratio is his famous paintings.

Figure-2: Greek Architecture 
Figure-3: Pyramids of Giza 
Figure-4: Mona Lisa
Golden ratio is not only hidden in man-made objects, but also in the nature. The ratio of the height between our head and stomach, to the height between our stomach to foot is about 1.6. This is near to the value of golden ratio. Also, the ratio between the length of shoulder-to-elbow and elbow-to-finger tips is in golden ratio. Moreover, different segments of our fingers follow the golden ratio.
Golden Ratio – Definition
If the ratio between any two natural numbers, is equal to the ratio of the sum of those two numbers to the greater number among them, then it is known as golden ratio.
Let “a” and “b” be two natural numbers and “a” be greater than “b“; then,
The Golden Ratio φ = a/b = (a + b)/a = 1.6180339887498948 … (where, a > b )
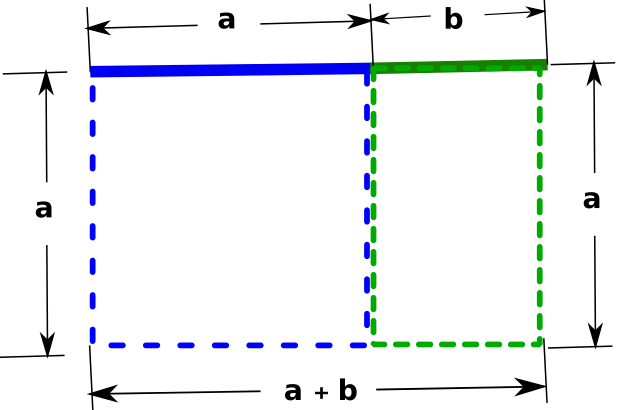
For example, let us consider the following figure:

The line shown in the above figure-5 is split in to two parts. The longer segment “a” is shown in blue color, whereas the shorter segment “b” in green. If the ratio of “a” to “b” is equal to the ratio of (a+b) to a, (that is, a:b = (a+b):a), then the ratio is said to be golden ratio.
Suppose, the line segments “a” and “b” shown in the above figure, are extended to form a square (blue color region) and a rectangle (green color region). In this case, if the ratio of side (“a“) of green square to breadth (“b“) of blue rectangle, that is a:b, is equal to the ratio of length of the larger rectangle “a+b” (comprising both blue and green regions) to its breadth “a” , then the larger rectangle is said to be in golden ratio. That means, a/b = (a+b)/a = 1.61803…
Fibonacci Number Sequence
There is a strong relationship between the golden ratio and the Fibonacci number sequence. Before delving in to the details of this relationship, let us see, what the Fibonacci number sequence is? The Fibonacci number sequence is given below:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 …
This number sequence shows same pattern except the first two numbers 0 and 1. That is, every third number is the sum of the preceding two numbers.
For instance,
- 0 + 1 = 1
- 1 + 1 = 2
- 1 + 2 = 3
- 2 + 3 = 5
- 3 + 5 = 8
- 5 + 8 = 13
- 8 + 13 = 21
- 13 + 21 = 34
- 21 + 34 = 55 …
Now, let us find out the relationship between the Fibonacci numbers and the golden ratio.
The ratio between two consecutive numbers in the Fibonacci number sequence is approximately equal to the Golden Ratio (φ).
For instance, the ratio of 5 to 3 is, 1.666. The ratio between 55 and 34 is, 1.617. Similarly, the ratio of 233 to 144 (233/144) is, 1.618055… If we keep calculating the ratios in the same way for the greater numbers, we will get a ratio that is exactly equal to the golden ratio φ.
The Fibonacci number sequence can be visualized as shown below:
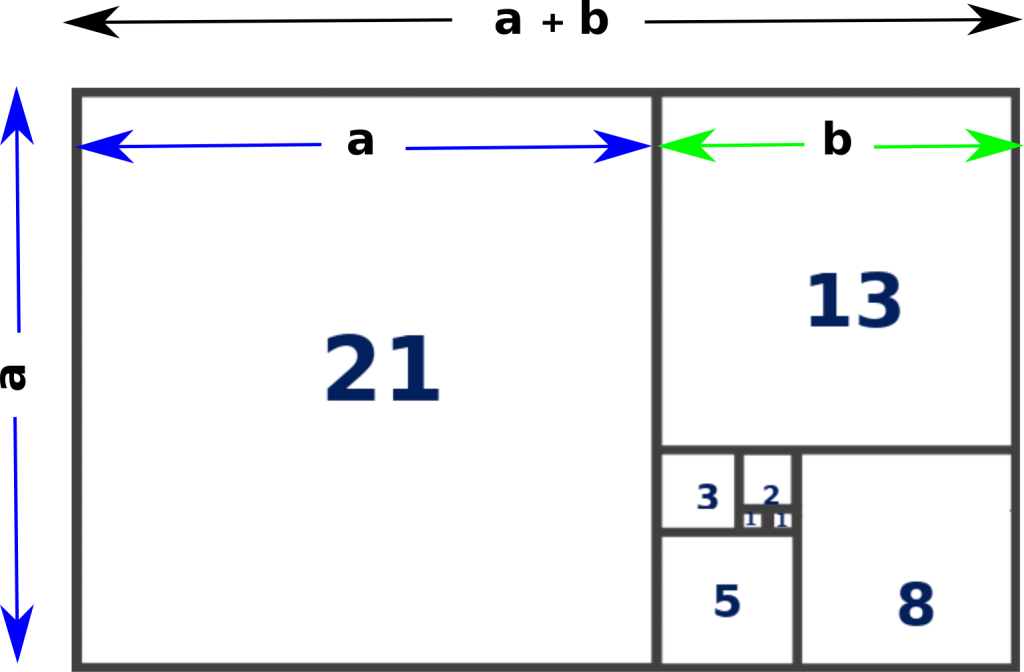
We can keep on drawing the rectangles (Figure-7) for the Fibonacci numbers using the golden ratio rectangle (Figure-6). Drawing arcs with sides of the squares as radii and connecting those arcs, Figure-7 will be like Figure-8 shown below. This kind of spiral form is visible in many things in nature, as well as in man-made objects.
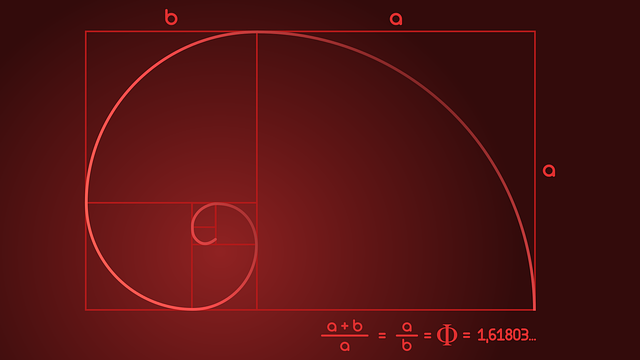
Golden Ratio and Fibonacci Number Sequence in Nature and Man-made things
The spiral form is visible in conch, spiral stairs, shells, hurricanes, spiral galaxies, etc. The number of petals in some flowers follow Fibonacci sequence. Also, the seeds in sunflower follow this pattern!








Be the first to comment